
Therefore, the coordinates of the midpoint are (7, 8). Similarly, the y-coordinate of the midpoint is the average of the y-coordinates of the end points here, this average is (1 + 15)/2 = 8. The x-coordinate of the midpoint is the average of the x-coordinates of the end points here, this average is (4 + 10)/2 = 7. You find the coordinates of the midpoint by averaging the values they give you. You will be given the two endpoints of the segment - for example, (4, 1) and (10, 15). Occasionally, the GMAT will ask to you to find the coordinates of the midpoint of a segment. If this is a new idea to you, or one which learned but forget a long time ago, then I strongly recommend you actually get some graph paper and actually graph sets of perpendicular lines and find their slopes, so you have a visual understanding of this idea. If you know the slope of one line, you flip that fraction over and change its sign to the opposite to make the slope of the perpendicular line. If one line has a slope of –3, the perpendicular line has a slope = +1/3. If one line has a slope = +4/7, then the perpendicular line has a slope = –7/4.
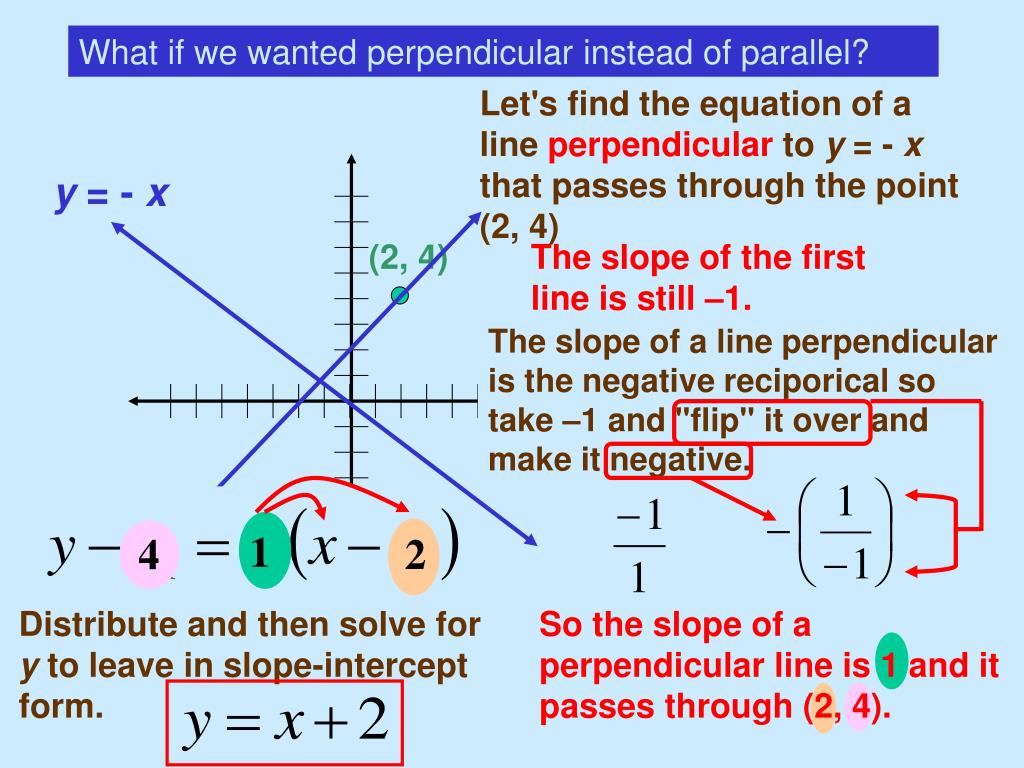
More elegantly, perpendicular slopes are opposite reciprocals. Now, put these two facts together - when line #1 has a slope, and line #2 is perpendicular to it, the slope of line #2 must have both the opposite sign from and must be a reciprocal of the original slop of line #1. For example, 2/5 and 5/2 are reciprocals 3/11 and 11/3 are reciprocals 7 and 1/7 are reciprocals. When the numerator and denominator of a fraction switch places, that’s called a reciprocal. In other words, the rise of one is the run of the other! When we go from the original line to a line perpendicular to it, the rise and the run switch places in the slope fraction. Because the triangle are congruent, the corresponding lengths are equal: AC = AD and BC = DE. But notice that these two triangles are congruent! Triangle ADE is just Triangle ACB rotated 90° around point A. The slope of line AB = (original rise)/(original run) = BC/AC, and the slope of line AE = (new rise)/(new run) = AD/DE. For each, we have constructed “rise over run” triangle for the slope. So, we have two perpendicular lines, the original line AB and the perpendicular line AE, intersecting at point A.
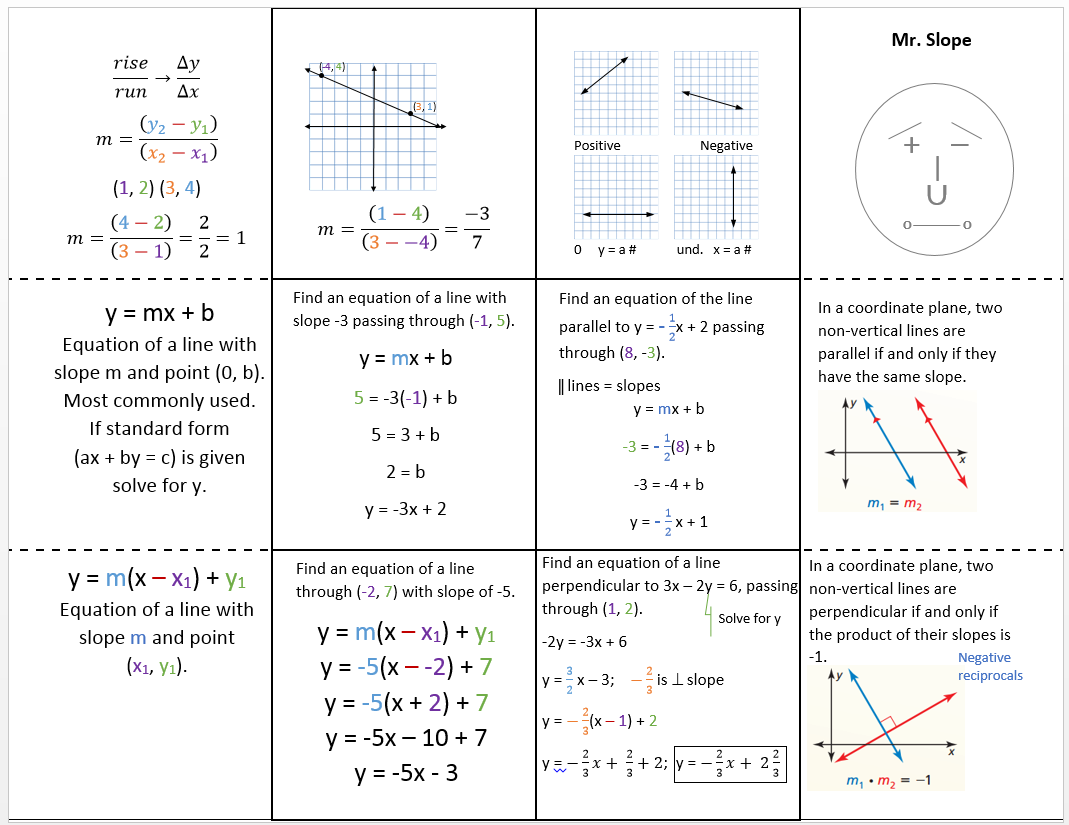
Let’s ignore ± signs for a moment, and just think about absolute values. Now, let’s think about if we take a “rise over run triangle” and rotate it 90°. Thus, the slope of a perpendicular line is always has a sign opposite of the sign of the original line. Similarly, if the original line has a negative slope, the perpendicular would have to have a positive slope. moving down to the right, moving up to the left). moving up to the right) - then the line perpendicular to it will have to have a negative slope (i.e. Consider any slanted line with a positive slope (i.e. The case with perpendicular lines is a little trickier. If the think about what the slope means geometrically, you will see that this has to be true. Parallel lines in the x-y plane have equal slope. I would strongly recommend against saying that either has “no slope”, because that is a term ripe for confusion: does “no slope” mean a slope with a value of zero or does it mean not being able to compute the value of the slope? I recommend that you absolutely banish the term “no slope” from your vocabulary. Vertical lines have an undefined slope: the value of their slope does not make any mathematical sense. Horizontal lines have a slope equal to zero. This means, vertical lines have undefined slope very roughly, we can think of vertical lines as having “infinite” slope, although technically, that way of interpreting vertical lines does not bear rigorous analysis of the idea of infinity - which, of course, is well beyond anything on the GMAT. By contrast, a vertical line is all rise and no run - when we calculate its rise over run, we get a mathematical error, because we can’t divide by zero. In the previous post, I discuss the idea of slope, but I didn’t talk about the special cases of horizontal and vertical lines.Ī horizontal line is all run and no rise: therefore, its slope, its rise/run, is zero. What is the slope of the median from A to the midpoint of BC?
#PARALLEL AND PERPENDICULAR LINES FULL#
Lines P & Q have a single intersection point - what is the full set of possible quadrants in which the intersection point could be?ģ) The median of a triangle is the line from any vertex to the midpoint of the opposite side. The two slopes and the two y-intercepts are four different numbers, none equal. Line Q also has a positive slope and a positive y-intercept. Which of the following lines is perpendicular to Line A?Ģ) Line P has a positive slope and a positive y-intercept. By Mike MᶜGarry on Novem, UPDATED ON January 15, 2020, in GMAT Geometryġ) Line A has the equation 3x + y = 7.


 0 kommentar(er)
0 kommentar(er)
